Ray marching is a useful technique for rendering complex scenes, but what if you want that scene repeated throughout space, infinitely in all directions?

Ray Marching
Ray marching is a rendering technique often used implemented in shader demos. Similar to ray tracing, it projects a ray from the camera to find the geometry that it intersects. The difference is that instead of casting an infinite ray through the scene and finding the closest intersection, the ray is advanced by the smallest distance that will not intersect any geometry. When that distance drops below a certain threshold, the ray is considered to have intersected the geometry. In this way, the ray is stepped (“marched”) forward through space until an intersection is found.
Because ray marching only requires calculation of the distance between a point and a surface, not the intersection of a line and a surface, it may be easier to calculate.
For an in-depth explanation of ray marching, see the excellent video tutorial series by Art of Code.
Infinitely Tiling Space – The Cheap Way
Given that your geometry is confined to a cube (0, 0, 0) to (1, 1, 1), the easiest way to have your geometry repeat infinitely is to simply take the current ray position modulo 1 before testing it against the geometry.
This works if your scene is small compared to the cube. If your scene is up to about a third of the size of the cube then it will appear okay, however you will start getting artefacts beyond that. This is because for large objects, the ray may start inside an object.
If having the scene small is an acceptable compromise, this way is much faster to compute.
Infinitely Tiling Space – The Proper Way
The solution to correctly tiling in space is quite simple – test for intersection with the bounding volume as well as the scene geometry. If the ray intersects the bounding volume then simply wrap it using the modulus operator and continue marching.
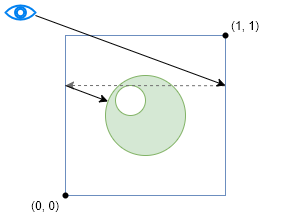
Testing for intersection with the unit bounding cube is simple: because it is axis-aligned, it can be decomposed into six intersections with axis-aligned infinite planes, meaning that each axis can be considered independently.
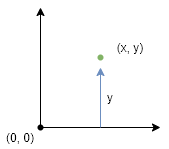
It is important that intersections are only registered when exiting the space, not when entering it, so the direction of the ray must also be considered. Otherwise, when the point was wrapped from the distal side, it would immediately collide with the proximal side.
GLSL code for finding the distance between the ray and the closest face on the unit cube is given below.
/**
* Find the shortest distance to the inside
* of an axis aligned unit cube.
*
* @param vec3 position The position of the ray to test.
* @param vec3 rayDirection The direction of the ray.
*
* @return float Returns the distance between the point and the cube.
*/
float unitSpaceDistance(vec3 position, vec3 rayDirection)
{
float dx, dy, dz;
if (rayDirection.x < 0.0)
dx = position.x;
else
dx = 1.0 - position.x;
if (rayDirection.y < 0.0)
dy = position.y;
else
dy = 1.0 - position.y;
if (rayDirection.z < 0.0)
dz = position.z;
else
dz = 1.0 - position.z;
return min(min(dx, dy), dz);
}The ray marching function must then be modified to consider intersections with both the scene geometry and the bounding volume:
/**
* March rays through an infinitely tiled unit space.
*
* @param vec3 rayOrigin The starting point of the ray (camera position).
* @param vec3 rayDirection The direction of the ray, in world space.
*
* @return vec3 Returns the distance from the ray origin at which the ray
* intersects the scene.
*/
float rayMarchUnitSpace(vec3 rayOrigin, vec3 rayDirection)
{
const int MAX_STEPS = 300;
const float RAY_INTERSECTION_DISTANCE = 0.001;
float distanceFromOrigin = 0.0;
float totalDistance = 0.0;
rayOrigin = mod(rayOrigin, 1.0);
int i;
for (i = 0; i < MAX_STEPS; ++i)
{
vec3 rayPosition = rayOrigin + distanceFromOrigin * rayDirection;
float surfaceDistance = getSurfaceDistance(rayPosition);
float unitSpaceDistance = unitSpaceDistance(rayPosition, rayDirection);
if (unitSpaceDistance < surfaceDistance)
{
distanceFromOrigin += unitSpaceDistance;
totalDistance += unitSpaceDistance;
if (unitSpaceDistance < RAY_INTERSECTION_DISTANCE || totalDistance > MAXIMUM_RAY_LENGTH)
{
rayOrigin = mod(rayOrigin + rayDirection * (distanceFromOrigin + RAY_INTERSECTION_DISTANCE), 1.0);
distanceFromOrigin = 0.0;
}
}
else
{
distanceFromOrigin += surfaceDistance;
totalDistance += surfaceDistance;
if (surfaceDistance < RAY_INTERSECTION_DISTANCE || totalDistance > MAXIMUM_RAY_LENGTH)
break;
}
}
if (i == MAX_STEPS)
return MAXIMUM_RAY_LENGTH;
return min(MAXIMUM_RAY_LENGTH, totalDistance);
}This code functions as follows:
Firstly, the ray origin is wrapped into modulo-1 space. This has the effect of bringing the camera into the unit space, if it is outside it.
Ray marching then proceeds as normal, however two distances are calculated: the distance to the geometry as usual, and the distance to the bounding volume.
If the ray intersects with the bounding volume, then it is moved forward by the intersection distance di to ensure that it passes outside the bounding volume, then wrapped back into unit space with the modulus operation.
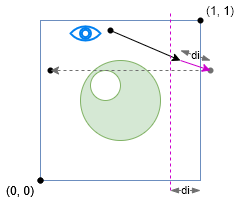
Notice in the figure how the ray has advanced to within the intersection distance di of the right-hand edge of the bounding area, but it has not actually passed the edge. If the modulus operation were to be applied now, the point would remain unmoved. To compensate for this, the ray is advanced by an additional di to ensure that it passes out of the bounding volume, and the modulus operation wraps it back to the inside.
Two distances are tracked, the current length of the ray, and the total length. The current length is used to keep track of the position while marching, and the total length is the final distance between the camera and the intersected surface.
This is all that is required. As long as the geometry fits within the unit cube, all the standard ray marching functions can be used.
The resulting shader is shown below. The source code can be found at https://www.shadertoy.com/view/3l3czB.